Can Focal Length Be Negative

Measure of how strongly an optical system converges or diverges light

"Rear focal distance" redirects here. For lens to pic distance in a camera, see Flange focal distance.

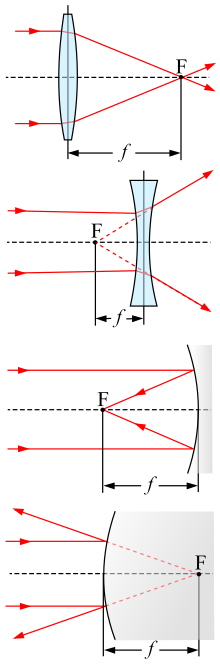
The focal bespeak F and focal length f of a positive (convex) lens, a negative (concave) lens, a concave mirror, and a convex mirror.

The focal length of an optical organisation is a measure of how strongly the organization converges or diverges lite; it is the inverse of the system's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the organisation diverges light. A organization with a shorter focal length bends the rays more sharply, bringing them to a focus in a shorter distance or diverging them more than rapidly. For the special case of a thin lens in air, a positive focal length is the distance over which initially collimated (parallel) rays are brought to a focus, or alternatively a negative focal length indicates how far in front end of the lens a betoken source must be located to form a collimated axle. For more full general optical systems, the focal length has no intuitive meaning; information technology is simply the inverse of the organisation's optical ability.

In nigh photography and all telescopy, where the subject is essentially infinitely far abroad, longer focal length (lower optical power) leads to college magnification and a narrower bending of view; conversely, shorter focal length or higher optical ability is associated with lower magnification and a wider bending of view. On the other paw, in applications such equally microscopy in which magnification is achieved by bringing the object shut to the lens, a shorter focal length (higher optical power) leads to college magnification because the subject can be brought closer to the centre of projection.

Thin lens approximation [edit]

For a thin lens in air, the focal length is the distance from the heart of the lens to the master foci (or focal points) of the lens. For a converging lens (for example a convex lens), the focal length is positive and is the distance at which a axle of collimated light will be focused to a single spot. For a diverging lens (for instance a concave lens), the focal length is negative and is the distance to the betoken from which a collimated axle appears to be diverging afterwards passing through the lens.

When a lens is used to form an prototype of some object, the distance from the object to the lens u, the distance from the lens to the prototype v, and the focal length f are related by

${\displaystyle {\frac {1}{f}}={\frac {1}{u}}+{\frac {1}{v}}\ .}$

The focal length of a thin convex lens can be easily measured past using it to grade an image of a afar light source on a screen. The lens is moved until a abrupt image is formed on the screen. In this case one / u is negligible, and the focal length is then given by

${\displaystyle f\approx 5\ .}$

Determining the focal length of a concave lens is somewhat more difficult. The focal length of such a lens is considered that bespeak at which the spreading beams of light would meet before the lens if the lens were not there. No image is formed during such a test, and the focal length must exist adamant by passing light (for case, the light of a light amplification by stimulated emission of radiation beam) through the lens, examining how much that lite becomes dispersed/ bent, and following the beam of light backwards to the lens's focal signal.

Full general optical systems [edit]

For a thick lens (i which has a non-negligible thickness), or an imaging system consisting of several lenses or mirrors (e.g. a photographic lens or a telescope), the focal length is often called the effective focal length (EFL), to distinguish it from other ordinarily used parameters:

• Front focal length (FFL) or front focal distance (FFD) (s _F) is the altitude from the forepart focal point of the system (F) to the vertex of the first optical surface (S₁).^{[one] [2]}
• Back focal length (BFL) or back focal distance (BFD) (southward′ _F′) is the distance from the vertex of the terminal optical surface of the arrangement (Southward₂) to the rear focal signal (F′).^{[1] [2]}

For an optical system in air, the effective focal length (f and f′) gives the altitude from the forepart and rear master planes (H and H′) to the respective focal points (F and F′). If the surrounding medium is not air, then the distance is multiplied past the refractive alphabetize of the medium (n is the refractive index of the substance from which the lens itself is made; n ₁ is the refractive index of whatever medium in forepart of the lens; north _ii is that of whatsoever medium in back of it). Some authors call these distances the front/rear focal lengths, distinguishing them from the front/rear focal distances, divers in a higher place.^[1]

In general, the focal length or EFL is the value that describes the power of the optical arrangement to focus low-cal, and is the value used to calculate the magnification of the arrangement. The other parameters are used in determining where an image will exist formed for a given object position.

For the case of a lens of thickness d in air ( n ₁ = n ₂ = 1), and surfaces with radii of curvature R _i and R _two, the effective focal length f is given by the Lensmaker's equation:

${\displaystyle {\frac {ane}{f}}=(northward-1)\left({\frac {one}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-one)d}{nR_{1}R_{2}}}\right),}$

where n is the refractive index of the lens medium. The quantity 1 / f is too known equally the optical power of the lens.

The respective front focal distance is:^[3]

${\displaystyle {\mbox{FFD}}=f\left(i+{\frac {(n-1)d}{nR_{2}}}\right),}$

and the dorsum focal distance:

${\displaystyle {\mbox{BFD}}=f\left(one-{\frac {(n-1)d}{nR_{1}}}\right).}$

In the sign convention used here, the value of R ₁ will exist positive if the first lens surface is convex, and negative if it is concave. The value of R ₂ is negative if the second surface is convex, and positive if concave. Note that sign conventions vary between different authors, which results in different forms of these equations depending on the convention used.

For a spherically curved mirror in air, the magnitude of the focal length is equal to the radius of curvature of the mirror divided by 2. The focal length is positive for a concave mirror, and negative for a convex mirror. In the sign convention used in optical design, a concave mirror has negative radius of curvature, so

${\displaystyle f=-{R \over 2},}$

where R is the radius of curvature of the mirror's surface.

See Radius of curvature (optics) for more information on the sign convention for radius of curvature used here.

In photography [edit]

28 mm lens

50 mm lens

70 mm lens

210 mm lens

An instance of how lens pick affects bending of view. The photos in a higher place were taken by a 35 mm camera at a fixed distance from the subject.

Images of blackness letters in a thin convex lens of focal length f are shown in red. Selected rays are shown for letters E, I and K in blueish, greenish and orange, respectively. Note that E (at 2f) has an equal-size, real and inverted image; I (at f) has its prototype at infinity; and Thousand (at

f / two ) has a double-size, virtual and upright image.

In this computer simulation, adjusting the field of view (past changing the focal length) while keeping the subject field in frame (by irresolute accordingly the position of the camera) results in vastly differing images. At focal lengths approaching infinity (0 degrees of field of view), the low-cal rays are nearly parallel to each other, resulting in the subject looking "flattened". At modest focal lengths (bigger field of view), the subject appears "foreshortened".

Camera lens focal lengths are unremarkably specified in millimetres (mm), but some older lenses are marked in centimetres (cm) or inches.

Focal length (f) and field of view (FOV) of a lens are inversely proportional. For a standard rectilinear lens, FOV = 2 arctan x / 2f , where x is the diagonal of the flick.

When a photographic lens is prepare to "infinity", its rear nodal point is separated from the sensor or flick, at the focal plane, by the lens'south focal length. Objects far abroad from the photographic camera then produce sharp images on the sensor or moving picture, which is also at the image aeroplane.

To return closer objects in precipitous focus, the lens must be adjusted to increase the distance between the rear nodal point and the film, to put the pic at the image plane. The focal length (f), the distance from the front nodal point to the object to photo (s ₁), and the altitude from the rear nodal bespeak to the image plane (south _ii) are and so related by:

${\displaystyle {\frac {i}{s_{one}}}+{\frac {ane}{s_{2}}}={\frac {1}{f}}.}$

As due south ₁ is decreased, s _two must be increased. For example, consider a normal lens for a 35 mm camera with a focal length of f = fifty mm. To focus a distant object (due south _ane ≈ ∞), the rear nodal point of the lens must be located a distance southward _two = fifty mm from the image airplane. To focus an object i thousand away (s ₁ = 1,000 mm), the lens must be moved two.half-dozen mm farther away from the image plane, to s ₂ = 52.vi mm.

The focal length of a lens determines the magnification at which it images distant objects. It is equal to the distance between the image plane and a pinhole that images distant objects the same size every bit the lens in question. For rectilinear lenses (that is, with no paradigm distortion), the imaging of distant objects is well modelled as a pinhole camera model.^[four] This model leads to the simple geometric model that photographers use for computing the angle of view of a camera; in this case, the angle of view depends only on the ratio of focal length to film size. In general, the angle of view depends also on the distortion.^[five]

A lens with a focal length about equal to the diagonal size of the film or sensor format is known every bit a normal lens; its bending of view is like to the angle subtended by a large-enough print viewed at a typical viewing altitude of the print diagonal, which therefore yields a normal perspective when viewing the print;^[6] this angle of view is almost 53 degrees diagonally. For total-frame 35 mm-format cameras, the diagonal is 43 mm and a typical "normal" lens has a 50 mm focal length. A lens with a focal length shorter than normal is oft referred to as a wide-bending lens (typically 35 mm and less, for 35 mm-format cameras), while a lens significantly longer than normal may be referred to as a telephoto lens (typically 85 mm and more, for 35 mm-format cameras). Technically, long focal length lenses are but "telephoto" if the focal length is longer than the concrete length of the lens, just the term is oft used to describe any long focal length lens.

Due to the popularity of the 35 mm standard, camera–lens combinations are often described in terms of their 35 mm-equivalent focal length, that is, the focal length of a lens that would take the same angle of view, or field of view, if used on a total-frame 35 mm camera. Utilise of a 35 mm-equivalent focal length is particularly common with digital cameras, which often employ sensors smaller than 35 mm film, and so require correspondingly shorter focal lengths to achieve a given angle of view, by a factor known as the crop gene.

Run into also [edit]

• Depth of field
• Dioptre
• f-number or focal ratio

References [edit]

1. ^ ^{a b c} John E. Greivenkamp (2004). Field Guide to Geometrical Eyes. SPIE Printing. pp. half dozen–9. ISBN978-0-8194-5294-8.
2. ^ ^{a b} Hecht, Eugene (2002). Eyes (4th ed.). Addison Wesley. p. 168. ISBN978-0805385663.
3. ^ Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. pp. 244–245. ISBN978-0805385663.
4. ^ Charles, Jeffrey (2000). Practical astrophotography . Springer. pp. 63–66. ISBN978-1-85233-023-i.
5. ^ Stroebel, Leslie; Zakia, Richard D. (1993). The Focal encyclopedia of photography (third ed.). Focal Press. p. 27. ISBN978-0-240-51417-8.
6. ^ Stroebel, Leslie D. (1999). View Camera Technique. Focal Press. pp. 135–138. ISBN978-0-240-80345-six.

Can Focal Length Be Negative,

Source: https://en.wikipedia.org/wiki/Focal_length

Posted by: dodsonbeele1989.blogspot.com

Share this post