Work Change In Kinetic Energy

Kinetic Energy and Work-Energy Theorem

The work-free energy theorem states that the work done by all forces acting on a particle equals the change in the particle's kinetic energy.

Learning Objectives

Outline the derivation of the piece of work-energy theorem

Primal Takeaways

Cardinal Points

The work W done by the net force on a particle equals the modify in the particle's kinetic energy KE:
$\text{W}=\Delta \text{KE}=\frac{ane}{ii} \text{mv}_\text{f}^two-\frac{1}{2} \text{mv}_\text{i}^2$
.
The work-energy theorem can exist derived from Newton'due south second law.
Piece of work transfers energy from one place to some other or one class to some other. In more than general systems than the particle organization mentioned here, work can modify the potential energy of a mechanical device, the estrus energy in a thermal organization, or the electric energy in an electrical device.

Central Terms

torque: A rotational or twisting effect of a forcefulness; (SI unit of measurement newton-meter or Nm; imperial unit of measurement foot-pound or ft-lb)

The Work-Energy Theorem

The principle of piece of work and kinetic energy (also known equally the work-energy theorem) states that the work done past the sum of all forces acting on a particle equals the change in the kinetic energy of the particle. This definition tin can be extended to rigid bodies by defining the work of the torque and rotational kinetic energy.

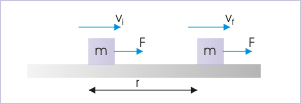
Kinetic Energy: A force does work on the block. The kinetic energy of the block increases as a result past the amount of work. This human relationship is generalized in the work-energy theorem.

The work W done by the internet force on a particle equals the alter in the particle'south kinetic free energy KE:

$\text{W}=\Delta \text{KE}=\frac{1}{two} \text{mv}_\text{f}^2-\frac{1}{two} \text{mv}_\text{i}^2$

where v_i and v_f are the speeds of the particle before and later the application of forcefulness, and m is the particle's mass.

Derivation

For the sake of simplicity, nosotros will consider the case in which the resultant force F is abiding in both magnitude and direction and is parallel to the velocity of the particle. The particle is moving with constant acceleration a along a direct line. The human relationship betwixt the cyberspace force and the acceleration is given by the equation F = ma (Newton's second police force), and the particle's deportation d, can be determined from the equation:

$\text{v}_\text{f}^2 = \text{five}_\text{i}^2 + ii\text{ad}$

obtaining,

$\text{d}=\frac{\text{v}_\text{f}^2-\text{five}_\text{i}^2}{2\text{a}}$

The piece of work of the net forcefulness is calculated as the product of its magnitude (F=ma) and the particle's deportation. Substituting the above equations yields:

$\text{W}=\text{Fd}=\text{ma}\frac{\text{v}_\text{f}^2-\text{v}_\text{i}^2}{2\text{a}}=\frac{1}{2} \text{mv}_\text{f}^2-\frac{ane}{2} \text{mv}_\text{i}^ii=\text{KE}_\text{f}-\text{KE}_\text{i}=\Delta \text{KE}$